Reservoir Sampling in MapReduce

[Image source]

We consider the problem of picking a random sample of a given size k from a large dataset of some unknown size n. The hidden assumption here is that n is large enough that the whole dataset does not fit into main memory, whereas the desired sample does.

Let's first review how this problem is tackled in a sequential setting - then we'll proceed with a distributed map-reduce solution.

Reservoir sampling

One of the most common sequential approaches to this problem is the so-called reservoir sampling. The algorithm works as follows: the data is coming through a stream and the solution keeps a vector of $k$ elements (the reservoir) initialized with the first $k$ elements in the stream and incrementally updated as follows: when the $i$-th element arrives (with $i \gt k$), pick a random integer $r$ in the interval $[1,..,i]$, and if $r$ happens to be in the interval $[1,..,k]$, replace the $r$-th element in the solution with the current element.

A simple implementation in Python is the following. The input items are the lines coming from the standard input:

# reservoir_sampling.py

import sys, random

k = int(sys.argv[1])
S, c = [], 0

for x in sys.stdin:
  if c < k: S.append(x)
  else:
    r = random.randint(0,c-1)
    if r < k: S[r] = x
  c += 1

print ''.join(S),

You can test it from the console as follows to pick 3 distinct random numbers between 1 and 100:

for i in {1..100}; do echo $i; done | python ./reservoir_sampling.py 3

Why does it work? The math behind it(*)

(Feel free to skip this section if math and probability are not your friends)
Let's convince ourselves that every element belongs to the final solution with the same probability.
Let $x_i$ be the $i$-th element and $S_i$ be the solution obtained after examining the first $i$ elements. We will show that $\Pr[x_j \in S_i] = k/i$ for all $j\le i$ with $k\le i\le n$. This will imply that the probability that any element is in the final solution $S_n$ is exactly $k/n$.
The proof is by induction on $i$: the base case $i=k$ is clearly true since the first $k$ elements are in the solution with probability exactly 1. Now let's say we're looking at the $i$-th element for some $i>k$. We know that this element will enter the solution $S_i$ with probability exactly $k/i$. On the other hand, for any of the elements $j\lt i$, we know that it will be in $S_i$ only if it was in $S_{i-1}$ and is not kicked out by the $i$-th element. By induction hypothesis, $\Pr[x_j \in S_{i-1}]= k/(i-1)$, whereas the probability that $x_j$ is not kicked out by the current element is $(1-1/i) = (i-1)/i$. We can conclude that $\Pr[x_j \in S_{i}] = \frac{k}{i-1}\cdot\frac{i-1}{i} = \frac{k}{i}$.

MapReduce solution

How do we move from a sequential solution to a distributed solution?
To make the problem more concrete, let's say we have a number of files where each line is one of the input elements (the number of lines over all files sum up to n) and we'd like to select exactly k of those lines.

The Naive solution

The simplest solution is to reduce the distributed problem to a sequential problem by using a single reducer and have every mapper map every line to that reducer. Then the reducer can apply the reservoir sampling algorithm to the data. The problem with this approach though is that the amount of data sent by the mappers to the reducer is the whole dataset.

A better approach

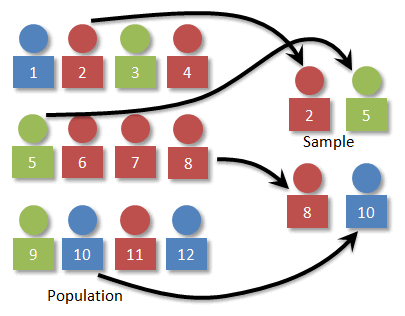
The core insight behind reservoir sampling is that picking a random sample of size $k$ is equivalent to generating a random permutation (ordering) of the elements and picking the top $k$ elements. Indeed, a random sample can be generated as follows: associate a random float id with each element and pick the elements with the $k$ largest ids. Since the ids induce a random ordering of the elements (assuming the ids are distinct), it is clear that the elements associated with the $k$ largest ids form a random subset.

We will start implementing this new algorithm in a streaming sequential setting. The goal here is to incrementally keep track of the $k$ elements with largest ids seen so far. A useful data structure that can be used to this goal is the binary min-heap. We can use it as follows: we initialize the heap with the first $k$ elements, each associated with a random id. Then, when a new element comes, we associate a random id with it: if its id is larger than the smallest id in the heap (the heap's root), we replace the heap's root with this new element.

A simple implementation in Python is the following:

# rand_subset_seq.py

import sys, random
from heapq import heappush, heapreplace

k = int(sys.argv[1])
H = []

for x in sys.stdin:
  r = random.random() # this is the id
  if len(H) < k: heappush(H, (r, x))
  elif r > H[0][0]: heapreplace(H, (r, x)) # H[0] is the root of the heap, H[0][0] its id
        
print ''.join([x for (r,x) in H]),

Again, the following test pick 3 distinct random numbers between 1 and 100:

for i in {1..100}; do echo $i; done | python ./rand_subset_seq.py 3

By looking at the problem under this new light, we can now provide an improved map-reduce implementation. The idea is to compute the ordering distributedly, with each mapper associating a random id with each element and keeping track of the top $k$ elements. The top $k$ elements of each mapper are then sent to a single reducer which will complete the job by extracting the top $k$ elements among all. Notice how in this case the amount of data sent out by the map phase is reduced to the top $k$ elements of each mapper as opposed to the whole dataset.

An important trick that we can use is the fact that Hadoop framework will automatically present the values to the reducer in order of keys from lowest to highest. Therefore, by using the negation of the id as key, the first $k$ element read by the reducer will be the top $k$ elements we are looking for.

We now provide the mapper and reducer code in Python language, to be used with Hadoop streaming.

The following is the code for the mapper:

#!/usr/bin/python
# rand_subset_m.py

import sys, random
from heapq import heappush, heapreplace

k = int(sys.argv[1])
H = []

for x in sys.stdin:
  r = random.random()
  if len(H) < k: heappush(H, (r, x))
  elif r > H[0][0]: heapreplace(H, (r, x))

for (r, x) in H:
  # by negating the id, the reducer receives the elements from highest to lowest 
  print '%f\t%s' % (-r, x),

The Reducer simply returns the first $k$ elements received.

#!/usr/bin/python
# rand_subset_r.py

import sys

k = int(sys.argv[1])
c = 0

for line in sys.stdin:
  (r, x) = line.split('\t', 1)
  print x,
  c += 1
  if c == k: break

We can test the code by simulating the map-reduce framework. First, add the execution flag to the mapper and reducer files (e.g., chmod +x ./rand_subset_m.py and chmod +x ./rand_subset_r.py). Then we pipe the data to the mapper, sort the mapper output, and pipe it to the reducer.

k=3; for i in {1..100}; do echo $i; done | ./rand_subset_m.py $k | sort -k1,1n | ./rand_subset_r.py $k

Running the Hadoop job

We can finally run our Python MapReduce job with Hadoop. If you don't have Hadoop installed, you can easily set it up on your machine following these steps. We leverage Hadoop Streaming to pass the data between our Map and Reduce phases via standard input and output. Run the following command, replacing [myinput] and [myoutput] with your desired locations. Here, we assume that the environment variable HADOOP_INSTALL refers to the Hadoop installation directory.

k=10 # set k to what you need
hadoop jar ${HADOOP_INSTALL}/contrib/streaming/hadoop-*streaming*.jar \
-D mapred.reduce.tasks=1 \
-D mapred.output.key.comparator.class=org.apache.hadoop.mapred.lib.KeyFieldBasedComparator \
-D mapred.text.key.comparator.options=-n \
-file ./rand_subset_m.py -mapper "./rand_subset_m.py $k" \
-file ./rand_subset_r.py -reducer "./rand_subset_r.py $k" \
-input [myinput] -output [myoutput]

The first flag sets a single reducer, whereas the second and third are used to make Hadoop sort the keys numerically (as opposed to using string comparison).

Further notes

The algorithm-savvy reader has probably noticed that while reservoir sampling takes linear time to complete (as every step takes constant time), the same cannot be said of the approach that uses the heap. Each heap operation takes $O(\log k)$ time, so a trivial bound for the overall running time would be $O(n \log k)$. However, this bound can be improved as the heap replace operation is only executed when the $i$-th element is larger than the root of the heap. This happens only if the $i$-th element is one of the $k$ largest elements among the first $i$ elements, which happens with probability $k/i$. Therefore the expected number of heap replacements is $\sum_{i=k+1}^n k/i \approx k \log(n/k)$. The overall time complexity is then $O(n + k\log(n/k)\log k)$, which is substantially linear in $n$ unless $k$ is comparable to $n$.

What if the sample doesn't fit into memory?

So far we worked under the assumption that the desired sample would fit into memory. While this is usually the case, there are scenarios in which the assumption may not hold. Afterall, in the big data world, 1% of a huge dataset may still be too much to keep in memory!

A simple solution to generate large samples is to modify the mapper to simply output every item along with a random id as key. The MapReduce framework will sort the items by id (substantially, generating a random permutation of the elements). The (single) reducer can be left as is to just pick the first $k$ elements. The drawback with this approach is again that the whole dataset needs to be sent to a single reducer. Moreover, even if the reducer does not store the $k$ items in memory, it has to go through them, which can be time-consuming if $k$ is very large (say $k=n/2$).

We now discuss a different approach that uses multiple reducers. The key idea is the following: suppose we have $\ell$ buckets and generate a random ordering of the elements first by putting each element in a random bucket and then by generating a random ordering in each bucket. The elements in the first bucket are considered smaller (with respect to the ordering) than the elements in the second bucket and so on. Then, if we want to pick a sample of size $k$, we can collect all of the elements in the first $j$ buckets if they overall contain a number of elements $t$ less than $k$, and then pick the remaining $k-t$ elements from the next bucket. Here $\ell$ is a parameter such that $n/\ell$ elements fit into memory. Note the key aspect that buckets can be processed distributedly.

The implementation is as follows: mappers associate with each element an id $(j,r)$ where $j$ is a random index in $\{1,2,\ldots,\ell\}$ to be used as key, and $r$ is a random float for secondary sorting. In addition, mappers keep track of the number of elements with key less than $j$ (for $1\le j\le \ell$) and transmit this information to the reducers. The reducer associated with some key (bucket) $j$ acts as follows: if the number of elements with key less or equal than $j$ is less or equal than $k$ then output all elements in bucket $j$; otherwise, if the number of elements with key strictly less than $j$ is $t\lt k$, then run a reservoir sampling to pick $k-t$ random elements from the bucket; in the remaining case, that is when the number of elements with key strictly less than $j$ is at least $k$, don't output anything.

After outputting the elements, the mapper sends the relevant counts to each reducer, using -1 as secondary key so that this info is presented to the reducer first.

#!/usr/bin/python
# rand_large_subset_m.py

import sys, random
 
l = int(sys.argv[1])
S = [0 for j in range(l)]

for x in sys.stdin:
  (j,r) = (random.randint(0,l-1), random.random())
  S[j] += 1
  print '%d\t%f\t%s' % (j, r, x),

for j in range(l): # compute partial sums
  prev = 0 if j == 0 else S[j-1]
  S[j] += prev # number of elements with key less than j
  print '%d\t-1\t%d\t%d' % (j, prev, S[j]) # secondary key is -1 so reducer gets this first

The reducer first reads the counts for each bucket and decides what to do accordingly.

#!/usr/bin/python
# rand_large_subset_r.py

import sys, random

k = int(sys.argv[1])

line = sys.stdin.readline()
while line:
  # Aggregate Mappers information
  less_count, upto_count = 0, 0
  (j, r, x) = line.split('\t', 2)
  while float(r) == -1:
    l, u = x.split('\t', 1)
    less_count, upto_count = less_count + int(l), upto_count + int(u)
    (j, r, x) = sys.stdin.readline().split('\t', 2)
  n = upto_count - less_count # elements in bucket j

  # Proceed with one of the three cases
  if upto_count <= k: # in this case output the whole bucket
    print x,
    for i in range(n-1):
      (j, r, x) = sys.stdin.readline().split('\t', 2)
      print x,

  elif less_count >= k: # in this case do not output anything
    for i in range(n-1):
      line = sys.stdin.readline()

  else: # run reservoir sampling picking (k-less_count) elements
    k = k - less_count
    S = [x]
    for i in range(1,n):
      (j, r, x) = sys.stdin.readline().split('\t', 2)
      if i < k: 
        S.append(x)
      else:
        r = random.randint(0,i-1)
        if r < k: S[r] = x
    print ''.join(S),

  line = sys.stdin.readline()

The following bash statement tests the code with $\ell=10$ and $k=50$ (note the sort flag to simulate secondary sorting):

l=10; k=50; for i in {1..100}; do echo $i; done | ./rand_large_subset_m.py $l | sort -k1,2n | ./rand_large_subset_r.py $k

Running the Hadoop job

Again, we're assuming you have Hadoop ready to crunch data (if not, follow these steps). To run our Python MapReduce job with Hadoop, run the following command, replacing [myinput] and [myoutput] with your desired locations.

k=100000 # set k to what you need
l=50 # set the number of "buckets"
r=16 # set the number of "reducers" (depends on your cluster)
hadoop jar ${HADOOP_INSTALL}/contrib/streaming/hadoop-*streaming*.jar \
-D mapred.reduce.tasks=$r \
-D mapred.output.key.comparator.class=org.apache.hadoop.mapred.lib.KeyFieldBasedComparator \
-D stream.num.map.output.key.fields=2 \
-D mapred.text.key.partitioner.options=-k1,1 \
-D mapred.text.key.comparator.options="-k1n -k2n" \
-partitioner org.apache.hadoop.mapred.lib.KeyFieldBasedPartitioner \
-file ./rand_large_subset_m.py -mapper "./rand_large_subset_m.py $l" \
-file ./rand_large_subset_r.py -reducer "./rand_large_subset_r.py $k" \
-input [myinput] -output [myoutput]

Note how we enabled secondary key sorting as explained in the Hadoop streaming quickguide. Each map output record is composed of the bucket $j$, the random id $r$, and the rest. We use stream.num.map.output.key.fields sets the key to be the pair $(j, r)$. We use mapred.text.key.partitioner.options along with the -partitioner argument to partition only over $j$. Finally, we use mapred.text.key.comparator.options along with mapred.output.key.comparator.class to sort by $j$ in numerical order and then by $r$ again in numerical order.

Further notes

While this approach is general and can be used even in the case when $k$ is small, it still has the overhead of transmitting the whole dataset from the map phase to the reduce phase (although not to a single machine/reducer). When the sample fits in memory the other approach we discussed is faster and should be preferred.